
Picture of the clamp
By Jörg Brutscher (translation by Daniel Obee, edited by Jay Young)
Will this knot sling stop my fall?!? Who didn't ask himself this question while hanging a couple of meters above the last placed sling and facing the next dodgy move? To be able to judge the quality of such a placement was the objective of our research done at the TU Dresden. At the Saxon Elbsandstein, the Zittauer Mountains and in the Czech sandstone areas the rings in place, slung rocks or hourglasses and knot slings (knotted chord, crack slings) are the only protection used. The rings should be considered sufficiently strong to withstand every impact given. Rings that are dubious are scheduled to be replaced. Looking at slung rocks and hourglasses, the quality of the rock is crucial for the holding strength. Or - at small diameters - the strength of the cord, where it should be taken in account that the breaking strength given by the manufacturers is significantly reduced by the knots.
Until now, there was no conclusive research about the holding power of knotted chord placements. The available data mostly consisted of personal experience and views, anecdotes and the annual accident reports. There might have also been some non-systematic experiments done by the KTA in the late Seventies.
An obvious upper limit is the rated strength of the material. Besides that however, exists a broad range of often inconsistent experiences. Big whippers reportedly were held by 5mm slings in 'dubious placements' - while much stronger slings have broken out of 'didn't look that bad' placements.
What forces do falls generate?
The forces that occur at the last piece of pro in case of a fall were analysed by Mägdefrau . We confine our views to the most important results for climbing in the Elbsandstein, shown in two examples. One can assume that most climbing is done with a single rope. It's also assumable that, at the rings too, belay is done almost exclusively by body belay, Figure-of-Eight or HMS (Munter hitch).
Example 1: Belay with Figure-of-Eight, single rope, distance belay point to redirection point 3.8m, body weight 60 kg, climbing tower
| free falling distance (m) | falling distance (m) | Force at the highest piece (kn) |
| 0.8 | 1.55 | 2.8 |
| 1.2 | 2.25 | 3.1 |
| 1.6 | 2.9 | 3.35 |
| 2 | 3.7 | 3.8 |
Belaying directly off the power point or the use of twin ropes will slightly increase the forces. Of course, forces will increase with body weight.
Example 2: Belay off a fixed anchor, single rope, distance belay point to redirection point 8m, 4 additional running belays, friction on the rock, body weight 60 kg.
| free falling distance (m) | falling distance (m) | Force at the highest piece (kN) |
| 2 | 3 | 4.9 |
| 3.8 | 5.3 | 6.85 |
Forces above 10kN (=1000 kp) rarely occur in real life. This includes circumstances like: enormous falling distance accompanied by a high fall factor, static belay, high friction in the system or a stuck rope in the running belay, very high climbing weight.
The Experiment:
At the 'Institute für Werkstoffwissenschaft' of the University of Dresden experiments were performed with a tensile testing machine (FP 10). The focus of interest was on the breaking/holding power of different knots in relation to the narrowing. The tensile testing machine was capable of applying forces up to 10kN.

Picture of the clamp
Therefore, the experiment was restricted to forces below 10kN. Use of metal plates allowed us to adjust the constriction up to 12mm in steps of 0.5mm. The range between 2 and 10kN is the most interesting - crucial for the holding or not holding of knot slings. The influence of the constriction's shape could not to be tested as there was only a bench vice-type clamp available.
Sceme of the clamp
OverhandFigure-of-Eight (FoE)
single stranded Overhand
single stranded Figure-of-Eight
figure-of-nine
monkey head
Hole knot

For gauging, a particular clamp distance was set, the knot was placed and the force increased until either the knot slipped, the cord broke or the maximum force of 10kN was reached. The clamp distance was varied in steps of 0.5mm.
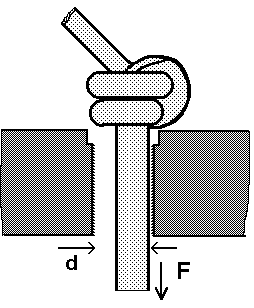
First, tests were made with Overhand knot and Figure-of-Eight with cord diameters from 3-7mm. At 5mm cord different knots were tested also, like the single-stranded Overhand and Figure-of-Eight, four-stranded Overhand and Figure-of-Eight, figure-of-nine (Figure-of-Eight, but with an additional wrap) and the Overhand. After all three, different types of webbing were also tested: 2x12mm, 1,4x23mm (backpack strap) and 3x25mm tubular webbing. The 5mm monkey head was already too bulky for the 12mm clamp distance and could not be torn through. It broke at 3.9 kN (single stranded). We abstained from testing the hole knot (similar to the one-stranded Figure-of-Eight but with 7 wraps), as it's holding capability is highly dependant on the shape of the hole and it's mostly used for (short) stances anyway. We also tested 1.5mm Kevlar technical cord (a better shoe lace). Six mm tech cord was only tested in two spot samples.
We assume a margin of error of around 0.05kN for the tensile testing machine and 0.5 mm for the clamps. The measured forces showed an increased statistical spread of +/- 10-20%. This might be caused by how the particular knot was knotted and placed. But the results are good enough to draw conclusions. The nominal breaking strength of cord (manufacturer information) is commonly about 200-250kN x d² (where d is diameter of the cord in mm). One should know that these ratings only apply to cord without knots. Knots may seriously reduce the breaking strength! Our experiments showed a reduction of breaking strength to 55% for the Overhand, to 60% for the Figure-of-Eight. Single stranded knots and webbing the ratings were even lower, at 35-45% original strength!
In testing we witnessed that the knots first thickened while constricting. Then the knots became thinner as the cord stretched itself. Random inspections showed 30% stretch before breaking. The thickening of the knot may result in knots holding in placements one could stick them in. The thinning results in a range where the force needed to pull the sling almost linearly increases with the reduction of the gap. From a certain clamp distance down, the knot will not pull through any more but break at a defined force.
The gap at which the knot stops slipping is dependent on the style of the knot. For the Figure-of-Eight one can assume a distance of about two times the diameter of the cord. Using the Overhand this distance is a little less, about 1.75. This must be reduced for single stranded knots to 1.5 (FoE) respectively 1.2 (Overhand). At higher cord diameters the ratio seems to decrease slightly.
Breaking strength of knotted chord/Webbing relative to the width of
the constriction at different material diameters. Filled symbols: cord
breaking, empty symbols: knot slipped. The short vertical line symbolizes
the closest gap through which the knot may be stuffed when loosely knotted.
Here the results 'Overhand 2-stranded' with different cord diameters.
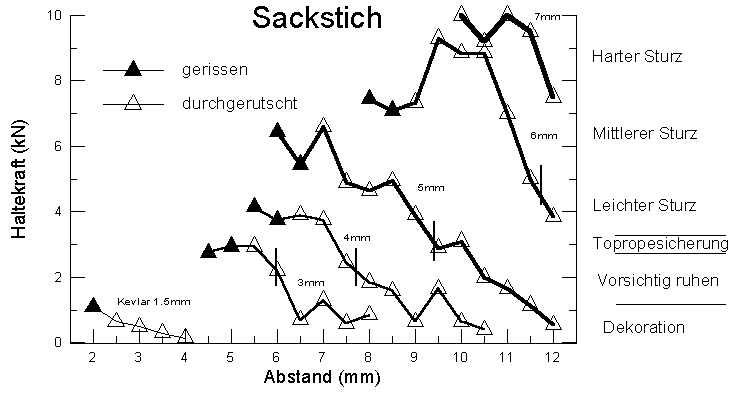
Here the results of 'FoE 2-stranded', with different cord diameters.
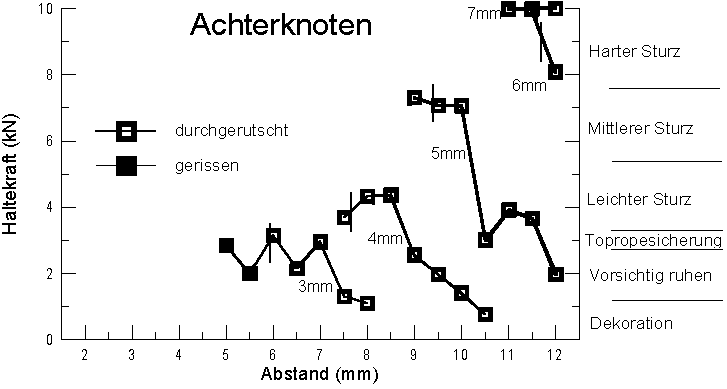
Here a comparison of different knots slung with 5mm cord. The Figure-of-Nine
('Neuner') is meant to be a FoE with one additional wrap.
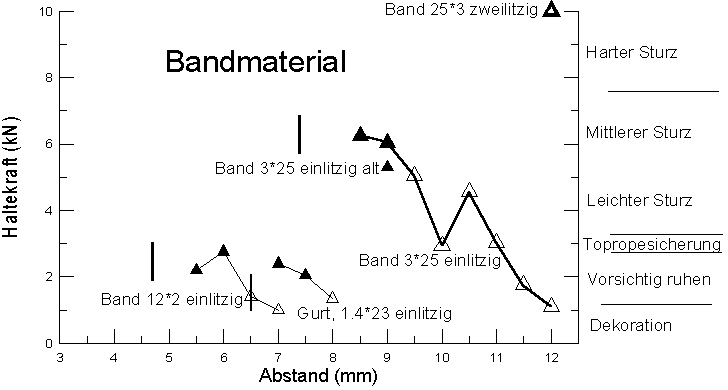
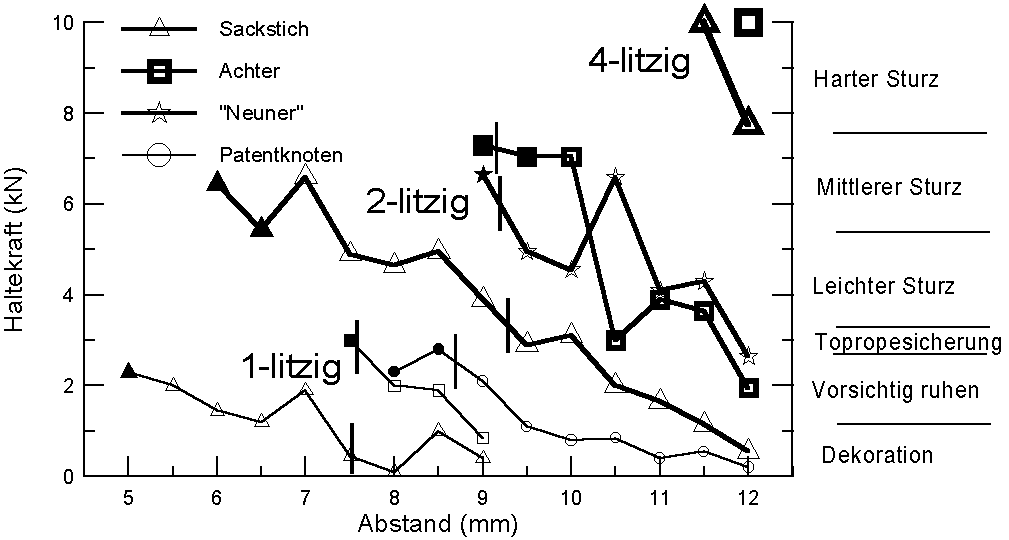
Here are the results of different webbings tested.
Which knot should be used, and when? Which knot is best suited to the task?
A good knot is characterized by its inability to tear through even wide constrictions even when set at a narrow profile. The cord should be chosen to withstand the applied forces. At this point it should be said that 3mm or 4 mm cord and single stranded webbing is only good for aiding. Single stranded knots should also not be used, as the reduction of breaking strength due to knotting is very high. They are better substituted by thinner but 2-stranded cord. While following the habit of knotting the inner strand of a sling at shallow constrictions it should be kept in mind that the breaking strength in this situation is reduced by half.
At cracks wider than 14mm and constrictions in the range of 6-20mm it should be no problem to make a good sling placement, but a certain constriction should be obligatory. The tails of the knot should always be long enough since the knots may roll. In addition, slings are easier to clean if the tails are a little longer. Principally one should use the biggest sling that passes through the expansion. The 2-stranded FoE is the knot of choice!
This is especially true for marginal constrictions. For those, it's also recommended to widen and flatten the knot before making the placement. Knotted webbing seems to be even better for marginal constrictions. Knots of wider webbing already reach their maximum holding power in places one could easily push them through. It might be interesting to examine the behaviour of even wider and more stable webbing (e.g. seatbelts). At very narrow constrictions knotted webbing is the best choice. At constrictions smaller than 2mm one-stranded webbing is the only option, but only suitable as rest point. With single stranded tubular webbing, placements might be capable of holding a couple of falls. 2-stranded Tubular webbing can be counted as a very decent placement. At small openings, webbing or 3mm cord might be tried. If a placement of single-stranded webbing is possible, this might at least hold a fall. If there's more room, usage of 5mm, 6mm or 7mm cord with FoE (double-stranded!) is recommended.
Openings wide enough to let an 11mm FoE slip through may be protected with a monkey head. A better bulk/expansion ratio is gained by material with a greater diameter (such as 18mm Kernmatel rope, sometimes available as boat equipment). Another suitable possibility is to knot a 4-stranded FoE with 11mm cord. The biggest possible knot is to fold a coiled rope in the middle, sling it with a prusik and place it as pro.
A rack of knotted cord should contain cord from 5-11mm gapless (preferably preknotted with FoE) and some tubular webbing. A reasonable add-on may consist of tubular webbing of 3 and 4mm and - to the upper end - of cord of 13-18mm.
How do knot slings perform in comparison to nuts and stoppers?
We'll skip the discussion about local climbing ethics. A chock is hard and smooth. Therefore the range between slipping and jamming is small. The range of <6mm to >30mm is covered better; chocks are easier and faster to place. Friends even allow placements in parallel cracks. A knot sling is softer and therefore provides a bigger surface. Therefore the danger of damaging soft rock is lower. Placing knot slings does take a little additional effort, and it is to keep in mind that there's a certain spectrum between a good placement and slipping. Knotted chord does provide a higher friction on the rock with the advantage of withstanding rope movement much better than a nut. Placements in open cracks and holes are possible where a stopper would fall out immediately.
The testing was made by Jörg Brutscher, André Hoose und Jens Freudenberger in January '97. Our thanks go out to the 'Institut für Werkstoffwissenschaft' for providing the tensile testing machine. Thanks also to Martin Lange for reviewing this paper. For further details please contact the author.
[1] See: Thesis Helmut Mägdefrau: Die Belastung des menschlichen Körpers beim Sturz ins Seil und deren Folgen, available at DAV Sicherheitskreis. Further information found in: Mehr Sicherheit beim Bergsport, Teil 10, Bayerisches Staatsministerium für Arbeit und Sozialordnung

And here the remains of the knot tests.
last edited 14.6.2005 Jörg Brutscher